Steve Hinchliffe and John Law
We are used to obscurely derived numbers dominating daily news. The FTSE, Dow Jones, bank lending rates, GDP, national debt – they creep into everyday conversation even if most of us have little idea about how they are created. But in the last few weeks they have all become dependent on another number, R0.
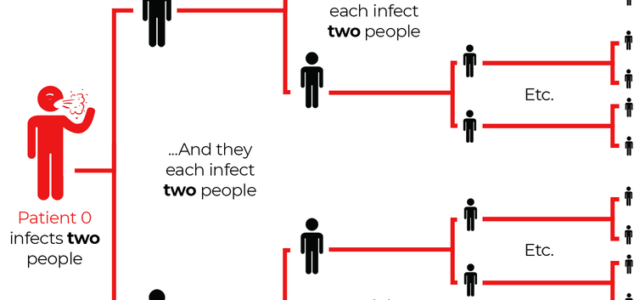
R0 is the epidemiologists’ ‘basic reproduction number’. With its roots in 1920s mathematical studies of epidemics, this expresses the average number of new infections derived from one existing infection. In its most basic form it is derived from ordinary differential equations that compare the total number of susceptible people, rates of infection and recoveries. If R0 is greater than 1 this tells us that infections are on the increase. When transmission falters, and R0 drops below 1, an end is in sight. The disease is petering out.
These numbers are central to public health planning and policy both prior to and during infectious disease outbreaks. Cutting transmission rates, with a lock down, or reducing the number of susceptible people, by vaccination or herd immunity, are examples of this model-driven logic.
In March, as transmission rates of the Covid-19 disease exceeded expectations, a revised calculation of R0 of between 2.4 and 3.1 came from modellers centred in Imperial College, London. This triggered, or justified, a UK Government shift from relatively low-key mitigation of the outbreak to one of suppression or lock down. As things progress, and as the disease starts to slow in the face of social distancing efforts, the reproduction number may also be instrumental in the shape and timing of an exit strategy.
The hope is that as R0 starts to drop, governments will start to implement a staggered return to school, work and relatively normal life. This ‘adaptive policy’ effectively takes the reproduction number, compares it to ICU hospital capacity, and judges at what level and when to relax social distancing measures. If transmission rates rise too high they can be used to trigger a temporary return to more stringent suppression. This may be repeated several times until a vaccine reduces the susceptible population (and so lowers R0 below 1).
Like many other indices R0 is extremely useful. This was certainly the case in the UK in March. But the trouble is that reliance on a single number can too easily reify or even fetishise R0. This is not a perfect pointer to the real world. No single number ever is, because the world is complicated, and those complications are both viral and social. This means that models and how we apply them are inherently social too and they need to be discussed and debated. There are at least two elements to this.
The first thing to say is that R0 numbers are unstable. Even a slight change in the latency or incubation period of a virus (or changes in whether people are exposed to the virus by those yet to show symptoms) can alter the reproduction number quite dramatically. Similarly, other parameters (from population size to assumptions about where and how people live) affect estimates of transmission rates. Given this sensitivity to starting assumptions, when R0 numbers become critical to people’s health, to jobs and to economies, it is vital to explore the assumptions made in models.
Secondly, the models are selective in how they represent lives. This can be a matter of life and death if a feted R0 number is used to relax an intervention. For example, most models assume populations are ‘panmictic’, or well-mixed. They assume, that is, that each member of the population is equally likely to come into contact with any other member. For rapid intervention this simplification is useful. At the same time, it is, of course, unrealistic.
As recent events have made clear, some groups, including many NHS staff, carers, delivery drivers, and frontline workers in supermarkets, are much more likely to be in virally meaningful contact with others. The R0 figures for these groups are likely to be high. And while the virus initially found the global travel and leisure activities of the relatively wealthy more than amenable to achieving pandemic status, a class divided island has become ideal for its persistence. Add to this the uneven pattern of multiple occupancy and multi-generational dwelling in parts of the UK, often organised along lines of both class and ethnicity, and we probably have seriously uneven R0s across the country. Emerging evidence that, despite higher mortality rates in older men, women are nevertheless more likely to be infected than men adds to this picture. While figures may be an artefact of testing regimes, they may also indicate that those traditionally carrying out caring duties are more exposed to the virus. R0 is both geographically uneven and socially patterned. It is viral, and it is also social.
So what does this mean for an exit strategy? The answer is that we need to be careful about using a single value for R0 as anything more than an index of the general direction of travel. In addition, we also need think about the social context, or choices, that are being embedded in models. Finally, we need to think about how lockdowns and their eventual remission may have quite different effects for different parts of society. The lesson is that policy makers will need more than models. To achieve fair and equitable outcomes they will also need to draw on other forms of expertise.
Steve Hinchliffe is Professor of Human Geography at the University of Exeter and currently sits on the UK Government’s Department of Environment, Food and Rural Affairs (DEFRA) Scientific Advisory Committee on Exotic Diseases and on Defra’s Science Advisory Group’s Social Science Expert Group. John Law is Emeritus Professor at the Open University and Visiting Professor at the Sámi Allaskuvla (Sámi University of Applied Sciences) in Guovdageaidnu, Finnmark, Norway. In 2015 he was awarded the J.D.Bernal Prize by the Society for Social Studies of Science.